Lesson 5 Double Counting
Motivating Example
The French nobleman (and avid gambler) Chevalier de Méré knew that betting on at least one six (⚅) in 4 rolls of a die was a favorable bet for him. Once other gamblers caught on, he devised a new bet: at least one double-six (⚅⚅) in 24 rolls of two dice. Although he did not know how to calculate the probabilities, he reasoned that the two bets should be equivalent, since
- double-sixes are \(1/6\) as likely as a single six,
- but there are \(6\) times as many rolls to compensate
Are the two bets equivalent?
Theory
Here is a common (but wrong) way of calculating the probability of getting at least one six in 4 rolls of a die.
\[\begin{align*} P(\text{at least one ⚅}) &= P(\text{⚅ on 1st roll, or ⚅ on 2nd roll, or ⚅ on 3rd roll or ⚅ on 4th roll}) \\ &= P(\text{⚅ on 1st roll}) + P(\text{⚅ on 2nd roll}) + P(\text{⚅ on 3nd roll}) + P(\text{⚅ on 4th roll}) \\ &= \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} \\ &= \frac{4}{6} ? \end{align*}\]
What’s wrong with the above reasoning? The problem is that \[ P(A \text{ or } B) \neq P(A) + P(B) \] in general. The reason is that \(P(A) + P(B)\) double counts outcomes where \(A\) and \(B\) both happen.
For example, suppose \(A\) is “⚅ on 1st roll” and \(B\) is “⚅ on 2nd roll”. Then, it is not hard to see that the event \(A \text{ or } B\) happens on 11 out of 36 outcomes, so \[ P(A \text{ or } B) = \frac{11}{36} \neq \frac{12}{36} = \frac{1}{6} + \frac{1}{6} = P(A) + P(B). \] \(P(A) + P(B)\) double counts the outcome where both rolls were ⚅s.
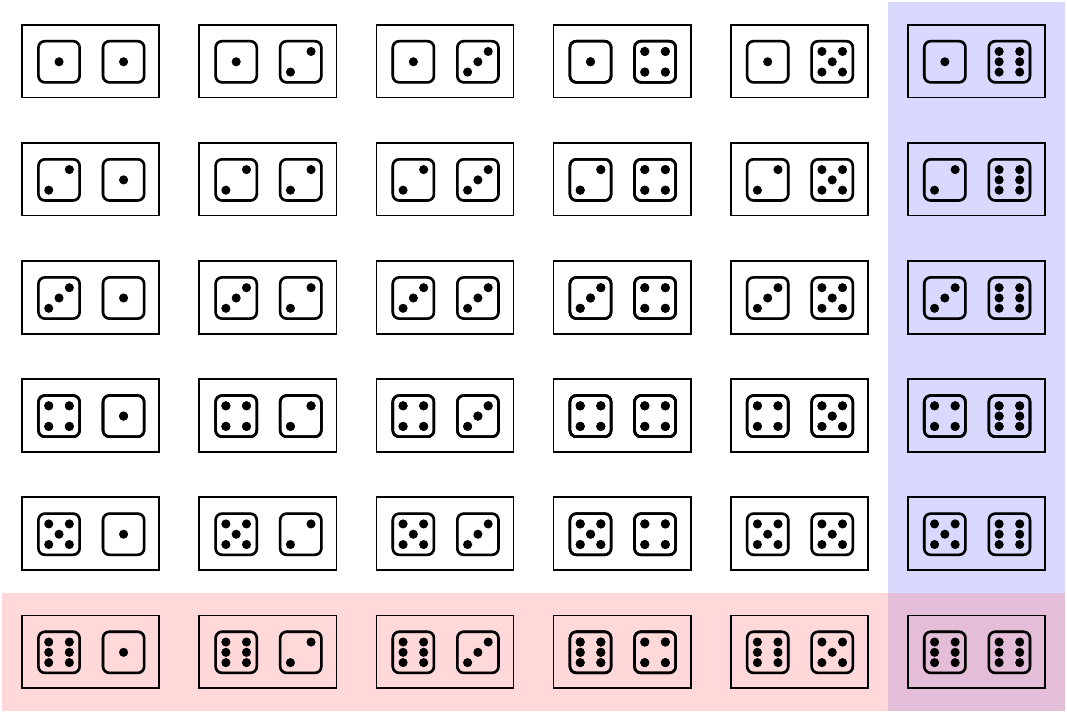
Figure 5.1: Double Counting Dice Rolls
One way to avoid double counting is to subtract the cases that are double counted.
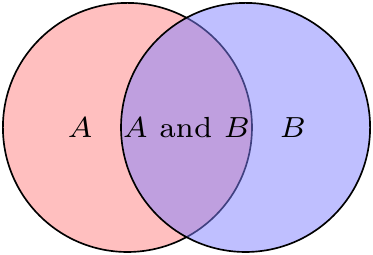
Figure 5.2: Intuition for the Inclusion-Exclusion Principle
So, for example: \[\begin{align*} P(\text{at least one ⚅ in 2 rolls}) &= P(\text{⚅ on 1st roll}) + P(\text{⚅ on 2nd roll}) - P(\text{⚅ on both rolls}) \\ &= \frac{1}{6} + \frac{1}{6} - \frac{1}{36} \\ &= \frac{11}{36} \end{align*}\]
However, this approach does not scale well to calculating the probability of at least one ⚅ in 4 rolls.
In many situations, it is easier to calculate the probability that an event does not happen, also known as the complement of the event. Because the total probability has to be 1, the two probabilities are related by the following formula.
Let’s apply the Complement Rule to the Chevalier de Méré’s problem. To calculate the probability of getting at least one ⚅ in 4 rolls, we can calculate the probability of the complement. If we did not get at least one ⚅, that must mean that we got no ⚅s. This means that every roll was one of the other 5 outcomes. This probability is much easier to calculate using the counting tricks we have learned. \[\begin{align*} P(\text{at least one ⚅}) &= 1 - P(\text{no ⚅s}) \\ &= 1 - \frac{5^4}{6^4} \\ &\approx 0.5177. \end{align*}\]
Examples
In poker, a “two pair” hand has 2 cards of one rank, 2 cards of another rank, and 1 card of a third rank. For example, the hand 2, 2, Q, Q, J is a “two pair”. Your friend calculates the probability of “two pair” as follows:
- There are \(\binom{52}{5}\) equally likely hands (where order does not matter).
- We count the number of ways to choose the first pair. There are \(13\) choices for the rank and \(\binom{4}{2}\) choices for the two cards within the rank, so there are \(13 \times \binom{4}{2}\) ways.
- Next, we count the ways to choose the second pair. Since one rank has already been chosen, there are \(12 \times \binom{4}{2}\) ways to do this.
- Finally, we choose the remaining card. There are \(11 \times \binom{4}{1} = 44\) ways to do this.
Your friend calculates the probability as \[ \frac{13 \times \binom{4}{2} \times 12 \times \binom{4}{2} \times 44}{\binom{52}{5}} \approx .095, \] but then finds online that the actual probability of “two pair” is only \(.0475\). This number is exactly half the probability that your friend got, so he suspects that he double-counted. But where?
Complete the calculation for the Chevalier de Méré. Calculate the probability of getting at least one ⚅⚅ in 24 rolls of two dice.