Lesson 31 Random Walk

Theory

The random walk (also known as the “drunkard’s walk”) is an example of a random process evolving over time, like the Poisson process (Lesson 17).

The setup for the random walk is as follows. A drunk man is stumbling home from a bar. Because of his inebriated state, each step he takes is equally likely to be one step forward or one step backward, independent of any other step.

In other words, the \(i\)th step is a random variable \(Z_i\), with p.m.f.

\[ \begin{array}{r|cc} z & -1 & 1 \\ \hline f(z) & 0.5 & 0.5 \end{array} \]

and the \(Z_i\)s are independent.

The drunkard’s position after \(n\) steps is \[ X_n = Z_1 + Z_2 + \ldots + Z_n. \] (We assume that he starts at the origin \(X_0 = 0\).)

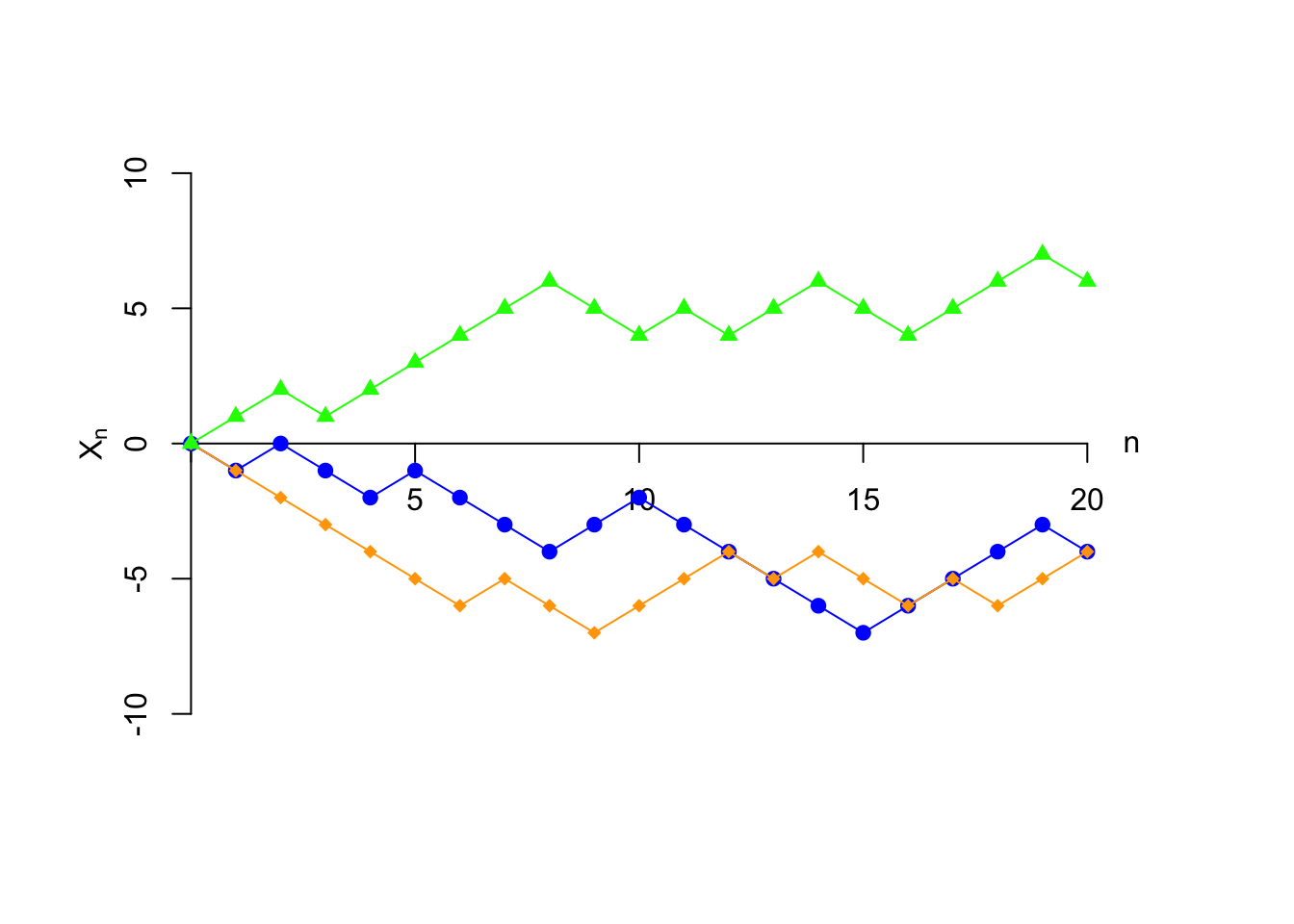
Shown below are three possible realizations of the random walk. A realization of a random process over time is called a sample path. We plot the three sample paths below, each of which shows the position of the drunkard \(X_n\) as a function of \(n\). Although all three sample paths start at 0 at \(n=0\), they diverge very quickly.

Essential Practice

Answer the following questions about the random walk. You should use linearity of expectation and properties of covariance as much as possible.

1. What is the distribution of \(X_2\), the drunkard’s position after just \(2\) steps? (This is not a named distribution. Just make a table showing the possible values and their probabilities.)
2. Calculate \(E[Z_i]\) and \(\text{Var}[Z_i]\).
3. Calculate \(E[X_3]\) and \(\text{Var}[X_3]\).
4. Consider \(X_3\) and \(X_5\). Do you think their covariance is positive, negative, or zero? Calculate \(\text{Cov}[X_3, X_5]\).