Lesson 34 Uniform Distribution
Motivation
How do we model a random variable that is equally likely to take on any real number between \(a\) and \(b\)?
Theory
The p.d.f. and c.d.f. are graphed below.
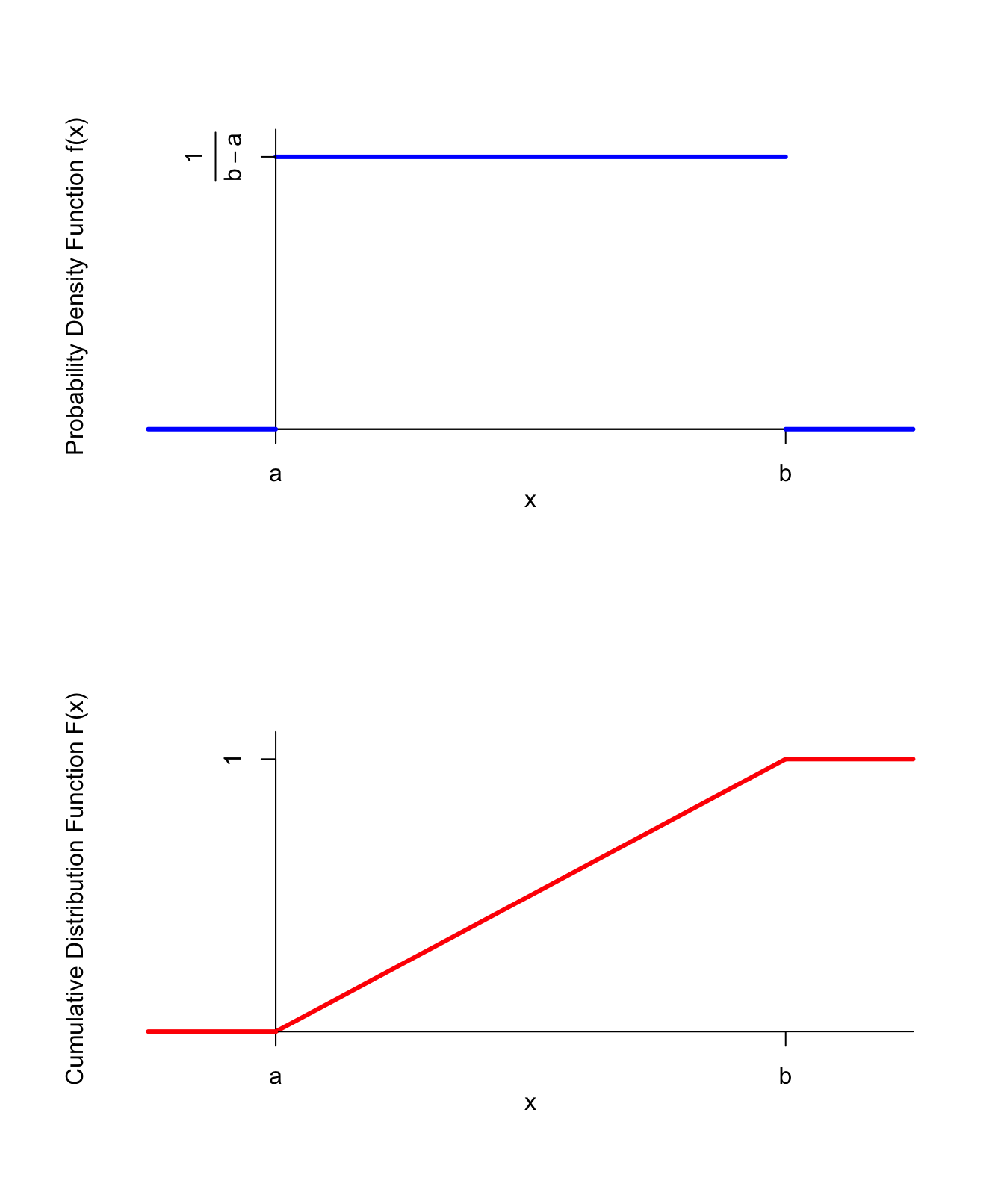
Figure 34.1: PDF and CDF of the Uniform Distribution
Why is the p.d.f. of a \(\text{Uniform}(a, b)\) random variable what it is?
- Since we want all values between \(a\) and \(b\) to be equally likely, the p.d.f. must be constant between \(a\) and \(b\).
- This constant is chosen so that the total area under the p.d.f. (i.e., the total probability) is 1. Since the p.d.f. is a rectangle of width \(b-a\), the height must be \(\frac{1}{b-a}\) to make the total area 1.
Essential Practice
A point is chosen uniformly along the length of a stick, and the stick is broken at that point. What is the probability the left segment is more than twice as long as the right segment?
(Hint: Assume the length of the stick is 1. Let \(X\) be the point at which the stick is broken, and observe that \(X\) is the length of the left segment.)
You inflate a spherical balloon in a single breath. If the volume of air you exhale in a single breath (in cubic inches) is \(\text{Uniform}(a=36\pi, b=288\pi)\) random variable, what is the probability that the radius of the balloon is less than 5 inches?