19  Expected Value

\[ \def\defeq{\overset{\text{def}}{=}} \def\E{\text{E}} \def\mean{\textcolor{red}{2.6}} \]

We define the expected value of a continuous random variable. To do this, we rely on intuition developed in Chapter 9, where expected value was defined for a discrete random variable.

19.1 Definition

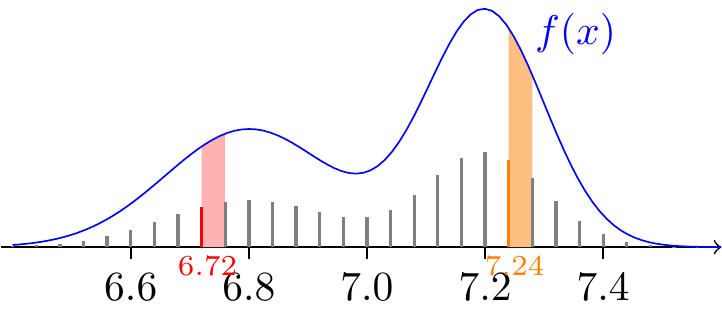
To motivate the definition of expected value for a continuous random variable, let’s consider how we might approximate it. Consider a continuous random variable \(X\) described by the PDF in Figure 19.1. If we chop up the \(x\)-axis finely enough, then we can approximate \(X\) by a discrete random variable that only takes on a discrete set of values. For example, we can represent all values in \(\textcolor{red}{[6.72, 6.76]}\) by \(\textcolor{red}{6.72}\) and all values in \(\textcolor{orange}{[7.24, 7.28]}\) by \(\textcolor{orange}{7.24}\), and we can ensure that the probability of each discrete outcome corresponds to the probability of the interval it represents.

Figure 19.1: Approximating the PDF (blue) by a PMF (gray)

Let \(\varepsilon\) be the spacing between values of this discrete random variable. In Figure 19.1, \(\varepsilon = 0.4\). The expected value of this discrete random variable can now be approximated as

\[ \begin{aligned} E[X] &\approx \sum_x x \cdot P(x < X \leq x + \varepsilon) \\ &\approx \sum_x x \cdot f(x) \varepsilon. \end{aligned} \]

In the second line, we used Equation 18.2. We know that we can make these approximations more accurate by chopping up the \(x\)-axis finer and finer, making \(\varepsilon\) smaller and smaller. In Figure 19.2, we get a better approximation by decreasing \(\varepsilon\) to \(0.2\) because \(\textcolor{red}{6.72}\) now only represents the smaller interval \(\textcolor{red}{[6.72, 6.74]}\) and \(\textcolor{orange}{7.24}\) only represents \(\textcolor{orange}{[7.24, 7.26]}\).

Figure 19.2: A better approximation of the PDF (blue) by a PMF (gray)

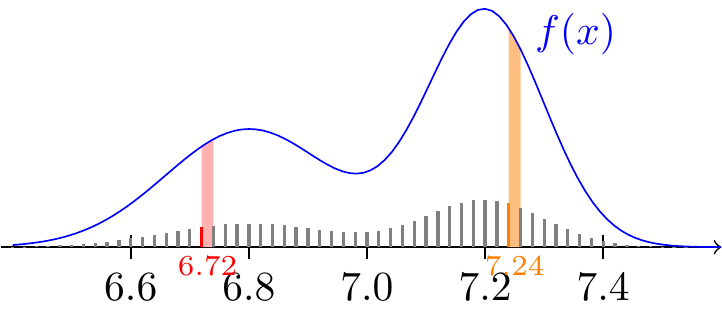
In the limit as \(\varepsilon \to 0\), this Riemann sum becomes an integral:

\[ \sum_x x \cdot f(x) \varepsilon \to \int_{-\infty}^\infty x f(x)\,dx. \]

This is the motivation behind the definition of the expected value of a continuous random variable.

Definition 19.1 The expected value of a continuous random variable \(X\) is \[ \E[X] \defeq \int_{-\infty}^\infty x f(x)\,dx. \tag{19.1}\]

Just as the expected value of a discrete random variable was where the PMF would balance, the expected value of a continuous random variable is where the PDF would balance on a scale. In other words, it is the center of mass.

Figure 19.3: The expected value is the center of mass.

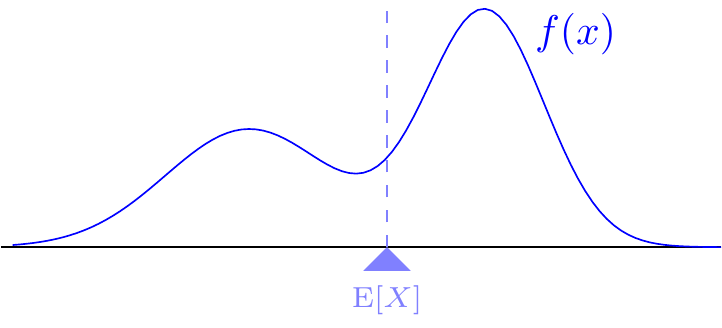
This center of mass interpretation can be used to bypass Equation 19.1 in some situations, as illustrated in the next example.

Example 19.1 (Expected Long Jump Distance) In Example 18.5, we examined a uniform model for \(X\), the distance of one of Joyner-Kersee’s long jumps. The PDF of \(X\) is \[ f(x) = \begin{cases} \frac{1}{1.2} & 6.3 < x < 7.5 \\ 0 & \text{otherwise} \end{cases}, \] which looks like this:

Under this model, what is \(\E[X]\), the expected distance of her long jump?

Because of symmetry, this PDF could only balance at the midpoint of the support, so the center of mass (and expected value) must be \[ \E[X] = \frac{6.3 + 7.5}{2} = 6.9\ \text{meters}. \]

We can check this answer using Equation 19.1: \[ \begin{aligned} \E[X] &= \int_{6.3}^{7.5} x \cdot \frac{1}{1.2}\,dx \\ &= \frac{1}{1.2} \frac{x^2}{2} \Big|_{6.3}^{7.5} \\ &= \frac{1}{1.2} \left( \frac{7.5^2}{2} - \frac{6.3^2}{2} \right) \\ &= 6.9, \end{aligned} \] but the center of mass interpretation allowed us to bypass the calculus.

However, in most situations, the center of mass will not be obvious, and we will need to use Equation 19.1 to determine the expected value.

19.2 Case Study: Radioactive Particles

Let’s apply Definition 19.1 to the Geiger counter example from Section 18.4.

Example 19.2 (Expected Time of First Arrival) What is the expected time of the first click, \(\E[T]\)?

In Example 18.9, we showed that the PDF of \(T\) is \[ f(x) = \begin{cases} \mean e^{-\mean x} & x > 0 \\ 0 & \text{otherwise} \end{cases}. \]

By Equation 19.1, the expected value is \[ \begin{aligned} \E[T] = \int_{-\infty}^\infty x f(x)\,dx &= \int_0^\infty x \cdot \mean e^{-\mean x}\,dx \\ &= \int_0^\infty u e^{-u} \frac{1}{\mean}\,du & (\text{substitute } u = \mean x) \\ &= \frac{1}{\mean} \Bigg( \underbrace{-ue^{-u} \Big|_0^\infty}_0 + \underbrace{\int_0^\infty e^{-u}\,du}_{1} \Bigg) & (\text{integration by parts}) \\ &= \frac{1}{\mean}. \end{aligned} \]

Only the first line involves probability concepts; the rest is just calculus. In the first line, we only integrated the PDF from \(0\) to \(\infty\) because the PDF \(f(x)\) is zero when \(x\) is negative.

Therefore, we expect the first click to happen in \(1/\mean \approx .38\) minutes. This makes sense, since clicks happen at a rate of \(\mean\) per minute.

Calculating the integral in Example 19.2 was rather messy. The next result makes expected values like this one easier to calculate. It is the direct analog of Proposition 9.1.

Proposition 19.1 (Tail Integral Expectation) Let \(X\) be a non-negative continuous random variable. Then,

\[ \E[X] = \int_0^\infty P(X > t)\,dt = \int_0^\infty (1 - F(t))\,dt. \tag{19.2}\]

Proof

Proof. If \(f(x)\) denotes the PDF of \(X\), then we can write \[ P(X > t) = \int_t^\infty f(x)\,dx. \] Substituting this into Equation 19.2, we obtain \[ \int_0^\infty P(X > t)\,dt = \int_0^\infty \int_t^\infty f(x)\,dx\,dt. \]

Now, we apply Fubini’s Theorem to change the order of integration. \[ \begin{aligned} &= \int_0^\infty \int_0^x f(x)\,dt\,dx \\ &= \int_0^\infty f(x) \underbrace{\int_0^x \,dt}_x\,dx \\ &= \int_0^\infty x f(x)\,dx \\ &= \E[X]. \end{aligned} \]

Let’s apply Proposition 19.1 to determine the expected time of the first arrival.

Example 19.3 Since \(T\) is a non-negative continuous random variable, we can apply Proposition 19.1. Note that we need the CDF of \(T\), which we derived in Example 18.8.

\[ \begin{aligned} \E[T] = \int_0^\infty (1 - F(t))\,dt &= \int_0^\infty (1 - (1 - e^{-\mean t}))\,dt \\ &= \int_0^\infty e^{-\mean t}\,dt \\ &= \frac{1}{\mean} \underbrace{\int_0^\infty \mean e^{-\mean t}\,dt}_{=1} \\ &= \frac{1}{\mean}. \end{aligned} \]

In the second-to-last step, we used a handy trick. We multiplied and divided by \(\mean\) so that inside the integral, we have the PDF of \(T\). The integral of any PDF over its support is 1. In a sense, we evaluated the integral using probability instead of calculus!

Another way to summarize a random variable is the median.

Definition 19.2 The median of a continuous random variable \(X\) is the value \(m\) such that \[ P(X \leq m) = P(X \geq m) = .5. \] That is, it is the value such that the random variable has equal probabilities of being above or below that value.

In the next example, we see that the median is not the same as the expected value (which is also called the mean).

Example 19.4 (The Median is Not the Mean) The median of \(T\) is defined to be the value of \(m\) such that \[ P(T \leq m) = .5. \]

There are many ways we could solve for \(m\), but perhaps the easiest is to observe that the left-hand side is just the CDF of \(T\) evaluated at \(m\).

Using the formula for the CDF we derived in Example 18.8, we need to solve \[ F(m) = 1 - e^{-\mean m}= .5 \] for \(m\).

Taking logarithms, we obtain: \[ m = -\frac{\log(.5)}{\mean} \approx .27. \] (Note that \(\log\) is the natural logarithm with base \(e\).)

So while the mean time until the first click is about .38 minutes, as we showed in Example 19.2, the median time until the first click is only .27 minutes. It makes sense that the mean is greater than the median because the mean is influenced by the small probability of extreme values.