23  Joint Distributions

$$

$$

$$$$

In this chapter, we describe the distributions of multiple continuous random variables. To get the most out of this chapter, please reread Chapter 13 to review how we described the distributions of multiple discrete random variables. You will see that many concepts are identical, except with PMFs replaced by PDFs and sums replaced by integrals.

23.1 Joint PDF

In Chapter 13, we described the distribution of two discrete random variables $X$ and $Y$ by their joint PMF $$f_{X,Y}(x,y)=P(X=x,Y=y).$$ The joint PMF is useless for continuous random variables $X$ and $Y$ because $$P(X=x,Y=y)=0$$ for any values $x$ and $y$. Instead, we shall describe the distribution of two continuous random variables by their joint PDF.

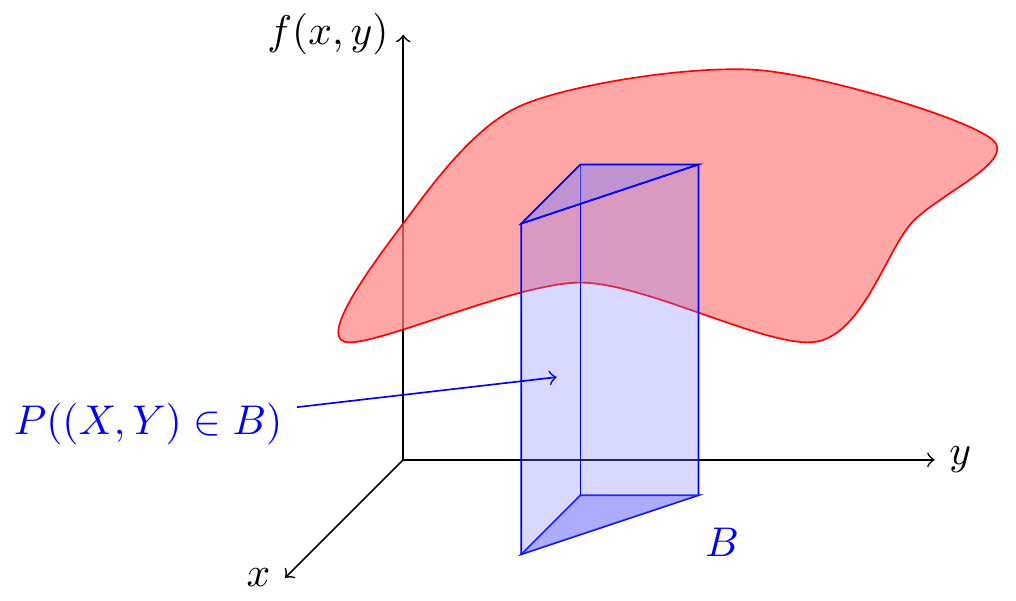
The joint PDF is the natural extension of the PDF (Chapter 18) to multiple random variables. Whereas a PDF $f_X(x)$ could be visualized as a curve; the joint PDF $f_{X,Y}(x,y)$ is a surface over the $xy$-plane, as shown in Figure 23.1.

Figure 23.1: The joint PDF of $X$ and $Y$

The probability of any event $B$ is the volume under this surface. We begin with an example where it is easy to determine this volume geometrically.

Example 23.1 (When Harry met Sally?) Harry and Sally plan to meet at Katz’s Deli for lunch. Let $X$ and $Y$ be the times that Harry and Sally arrive, respectively, in minutes after noon.

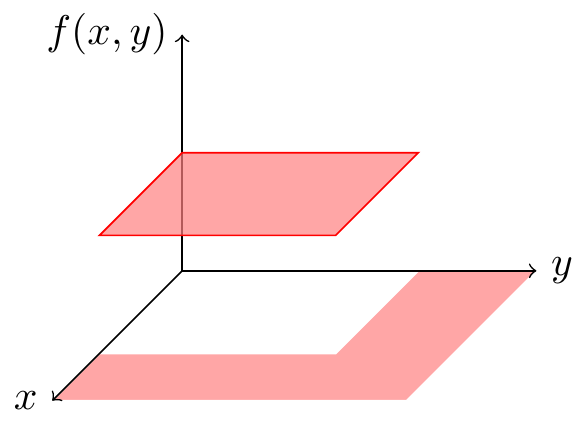
Suppose the joint PDF of $X$ and $Y$ is $$f_{X,Y}(x,y)=\{\begin{array}{ll}c,& 0\le x\le 30,0\le y\le 60\\ 0,& \text{else}\end{array},$$ where $c$ is a constant. That is, the surface is flat over the support of the distribution, as shown in Figure 23.2.

Figure 23.2: The joint PDF of $X$ and $Y$

In order to calculate any probabilities, we first need to determine the height of this surface. To do so, we use the fact that the total probability must be $1$; that is, the total volume under the surface must be $1$. Since the volume under the surface is a rectangular prism, its volume is $$\begin{array}{rl}\text{total volume under surface}& =\text{base}\cdot \text{height}\\ & =(30\cdot 60)\cdot c.\end{array}$$ Setting this total volume equal to $1$, we obtain $$c=\frac{1}{1800}.$$

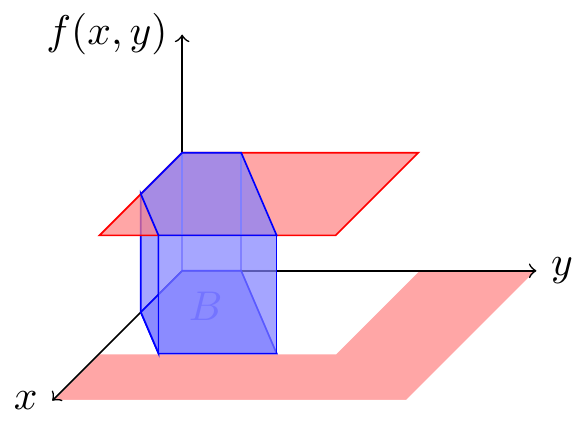
Using this information, we can calculate probabilities. For example, suppose Harry and Sally will each wait $15$ minutes for the other to arrive. What is the probability that they meet? In other words, we want to determine $$P((X,Y)\in B)=P(|X-Y|<15).$$

To do this, we determine the set $B$ in the $xy$-plane, and calculate the volume under the joint PDF above $B$, the blue prism shown in Figure 23.3.

Figure 23.3: The probability of the event $B$ where Harry and Sally arrive less than 15 minutes apart.

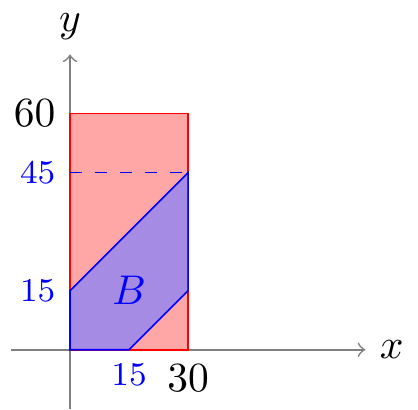
Figure 23.3 shows the full picture, but it is unwieldy to draw. For calculating probabilities, we usually just need a bird’s-eye view of the event $B$. Consider Figure 23.3 from the perspective of Rand the Raven, who is flying high above the $xy$-plane. The picture from Rand’s perspective is shown in Figure 23.4.

Figure 23.4: A bird’s-eye view of Figure 23.3.

To calculate the volume of the prism, we just need to determine the area of its base $B$ in Figure 23.4 and multiply by the height of the surface, $c=\frac{1}{1800}$. That is, $$\begin{array}{rl}P(|X-Y|<15)& =\text{volume under surface above }B\\ & =(\text{area of }B)\cdot \text{height of surface}\end{array}$$

The area of $B$ can be determined using basic geometry. One way is to take the area of the $30\times 45$ rectangle and subtract the areas of the two triangles. $$\begin{array}{rl}(\text{area of }B)& =30\cdot 45-\frac{1}{2}\cdot 30\cdot 30-\frac{1}{2}\cdot 15\cdot 15\\ & =787.5\end{array}$$

Therefore, the probability that Harry and Sally meet is $$P(|X-Y|<15)=787.5\cdot \frac{1}{1800}=.4375.$$

We were able to solve Example 23.1 using geometry because the joint PDF surface, $f_{X,Y}(x,y)$, was flat. However, in general, the joint PDF surface will be curved, and integration is necessary to calculate volumes under the surface. Specifically, we will need to calculate the double integral of the joint PDF over $B$:

$$P((X,Y)\in B)={\iint }_B{f}_{X,Y}(x,y)dxdy.$$

The next example illustrates how integration can be used to calculate a probability involving two random variables.

Example 23.2 (Blood Types) The ABO blood group system is used to classify human blood types. These blood types are caused by three genetic variants, or alleles, on chromosome 9: O, A, and B. The frequencies of these three alleles vary from population to population. In one population, it might be 70% O, 15% A, and 15% B, while in another population, it might be 60% O, 10% A, and 30% B.

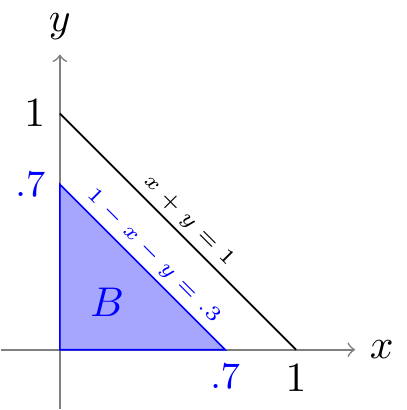
The frequencies of these three alleles in a population are random variables; let’s call them $X$, $Y$, and $Z$, respectively. The joint distribution of $X$ and $Y$ can be modeled by $$f(x,y)=\{\begin{array}{ll}12x^2& x,y>0,x+y<1\\ 0& \text{otherwise}\end{array}.$$ Note that $X+Y+Z=1$, so $Z$ is determined once we know $X$ and $Y$.

What is $P(Z>.3)=P(1-X-Y>.3)$, the probability that more than 30% of the alleles in a population will be B? To calculate this probability, we sketch a bird’s-eye view of the support of the distribution and the set $B=\{1-X-Y>.3\}$ in Figure 23.5.

Figure 23.5: Joint PDF of $X$ and $Y$, along with the event $B=\{1-X-Y>.3\}$.

The surface $f(x,y)$ is not flat, so to calculate the volume under the surface, we will need to calculate a double integral over $B$. To evaluate this integral, we convert the double integral into an iterated integral.

$$\begin{array}{rl}P(1-X-Y>.3)& ={\iint }_{B}f(x,y)dxdy\\ & ={\int }_0^{.7}\underset{4x^3{|}_0^{.7-y}}{\underbrace{{\int }_0^{.7-y}12x^{2}dx}}dy\\ & ={\int }_0^{.7}4(.7-y{)}^{3}dy\\ & =.2401.\end{array}$$

We would have arrived at the same answer if we had set up the iterated integral in the other order, $dydx$ instead of $dxdy$.

$$\begin{array}{rl}P(1-X-Y>.3)& ={\int }_0^{.7}{\int }_0^{.7-x}12x^{2}dydx\\ & ={\int }_0^{.7}12x^2{\int }_0^{.7-x}1dydx\\ & ={\int }_0^{.7}12x^2(.7-x)dx\\ & =.2401.\end{array}$$

So there is only about a $.24$ probability that the frequency of B alleles in a population exceeds 30%.

23.2 Marginal Distribution

In Section 13.2, we saw that we can recover the PMF of a discrete random variable $X$ from the joint PMF of $X$ and $Y$, by summing over all the possible values of $Y$: $$f_X(x)=\sum _y{f}_{X,Y}(x,y).$$

For continuous random variables, the idea is the same, except we integrate the PDF instead of summing the PMF.

Definition 23.1 (Marginal PDF) Let $f_{X,Y}(x,y)$ be the joint PDF of $X$ and $Y$. Then, the marginal PDF of $X$ is $$f_X(x)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_{X,Y}(x,y)dy.$$

The marginal PDF of $Y$, $f_Y(y)$, can be found similarly by integrating the joint PDF with respect to $x$.

Let us revisit Example 23.1 and determine the marginal distributions of the times that Harry and Sally arrive.

Example 23.3 (Marginal distribution of Harry’s and Sally’s arrival times) The marginal distribution of $X$, Harry’s arrival time after noon, is $$f_X(x)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_{X,Y}(x,y)dy={\int }_0^{60}\frac{1}{1800}dy=\frac{1}{30}$$ for $0<x<30$. We recognize this as the PDF of the $\text{Uniform}(a=0,b=30)$ distribution.

Similarly, the marginal distribution of $Y$, Sally’s arrival time after noon, is $$f_Y(y)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_{X,Y}(x,y)dx={\int }_{30}^{60}\frac{1}{1800}dx=\frac{1}{60}$$ for $0<y<60$. We recognize this as the PDF of the $\text{Uniform}(a=0,b=60)$ distribution.

That is, Harry is equally likely to arrive at any time between 12:30 and 1:00, and Sally is equally likely to arrive at any time between 12:00 and 1:00.

In Example 23.3, the joint PDF ends up being the product of the marginal PDFs: $$f_{X,Y}(x,y)=\frac{1}{1800}=\frac{1}{30}\cdot \frac{1}{60}=f_X(x)f_Y(y)$$ for $30<x<60,0<y<60$.

This proves to be a useful characterization of independence for continuous random variables.

Definition 23.2 (Joint PDF of independent random variables) Two continuous random variables $X$ and $Y$ are independent if their joint PDF is the product of the marginals: $$\begin{array}{}\text{(23.1)}& f_{X,Y}(x,y)=f_X(x)f_Y(y).\end{array}$$

Notice that for any events $A,B\in \mathbb{R}$, $$\begin{array}{rl}P(X\in A,Y\in B)& ={\iint }_{A\times B}{f}_{X,Y}(x,y)dydx\\ & ={\int }_A{\int }_B{f}_X(x)f_Y(y)dydx\\ & ={\int }_A{f}_X(x)\underset{P(Y\in B)}{\underbrace{{\int }_B{f}_Y(y)dy}}dx\\ & =P(Y\in B){\int }_A{f}_X(x)dx\\ & =P(Y\in B)P(X\in A),\end{array}$$ so this definition leads to all the properties of independence that we expect.

The next example illustrates the importance of respecting the support of the distribution when calculating marginal PDFs.

Example 23.4 (Marginal distribution of allele frequencies) In Example 23.2, we examined a particular model for the joint distribution of the allele frequencies of the O and A blood types.

The marginal distribution of $X$, the allele frequency of the O blood type, is $$f_X(x)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_{X,Y}(x,y)dy.$$

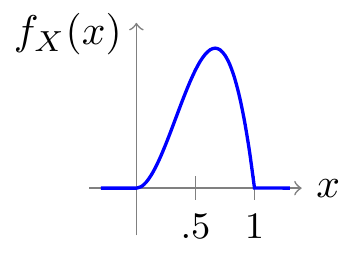
However, the support of this joint distribution is $$\{(x,y):x,y>0,x+y<1\}.$$ This support was illustrated in Figure 23.5. For a given value of $x$, the values of $y$ that are in the support are $(0,1-x)$. Therefore: $$\begin{array}{}\text{(23.2)}& f_X(x)={\int }_0^{1-x}12x^{2}dy=12x^2(1-x)0<x<1.\end{array}$$

Equation 23.2 is graphed in Figure 23.6. Populations are more likely than not to have more than 50% O alleles.

Figure 23.6: Marginal PDF of the allele frequency of the O blood type

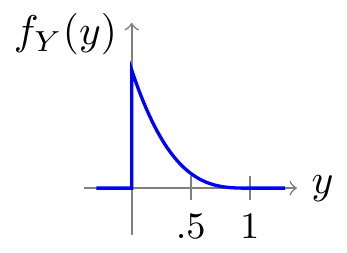
Similarly, the marginal PDF of $Y$, the frequency of the A allele, is $$\begin{array}{}\text{(23.3)}& f_Y(y)={\int }_0^{1-y}12x^{2}dx=4(1-y{)}^{3}0<y<1.\end{array}$$

Equation 23.3 is graphed in Figure 23.7. Populations are most likely to have a small frequency of A alleles.

Figure 23.7: Marginal PDF of the allele frequency of the A blood type

Notice that the product of the marginal PDFs is $$f_X(x)f_Y(y)=48x^2(1-x)(1-y{)}^3$$ for $0<x,y<1$, which is very different from the joint PDF $f_{X,Y}(x,y)$. Therefore, $X$ and $Y$ are not independent. This is intuitive because the frequencies of the alleles must add up to 1, so an increase in the frequency of one allele must be associated with a decrease in another.

23.3 Conditional Distribution

The conditional PDF is a way to describe information that one random variable provides about another. The definition of conditional PDF is the continuous analog of Definition 13.4.

Definition 23.3 (Conditional PDF) The conditional PDF of $X$ given $Y$ is $$f_{X\mid Y}(x\mid y)=\frac{f_{X,Y}(x,y)}{f_Y(y)},$$ provided $f_Y(y)\ne 0$.

Example 23.5 (Sally’s arrival time) Suppose Harry arrives at the deli at 12:15. What is the distribution of Sally’s arrival time, conditional on this information?

In other words, we want to know $f_{Y,X}(y\mid 15)$. Using our results from Example 23.3, $$f_{Y\mid X}(y\mid 15)=\frac{f_{X,Y}(15,y)}{f_X(15)}=\frac{1/1800}{1/30}=\frac{1}{60}$$ for $0<y<60$. Notice that this is the same as the marginal PDF $$f_Y(y).$$

In fact, for any $0<x<30$, $$f_{Y\mid X}(y\mid x)=\frac{1}{60}$$ for $0<y<60$. This means that regardless of Harry’s arrival time, Sally is equally likely to at any time between 12:00 and 1:00. In other words, their arrival times are independent!

Example 23.6 (Conditional frequencies of blood type alleles) In Example 23.2, we considered a model for the frequencies of the O and A blood type alleles.

If the frequency of the O blood type in a population is 60%, what is the distribution of the A blood type? By Definition 23.3, the conditional PDF of $Y$ given $X$ is $$f_{Y|X}(y|x)=\frac{f_{X,Y}(x,y)}{f_X(x)}=\frac{12x^2}{12x^2(1-x)}=\frac{1}{1-x}$$ for $0<y<1-x$. In particular, $f_{Y|X}(y|.6)=\frac{1}{.4}$ for $0<y<.4$, so the conditional distribution of $Y$ given $X=.6$ is $\text{Uniform}(a=0,b=.4)$.

On the other hand, if the frequency of the A blood type in a population is 30%, what is the distribution of the O blood type? By Definition 23.3, the conditional PDF of $X$ given $Y$ is $$f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}=\frac{12x^2}{4(1-y{)}^3}$$ for $0<x<1-y$. In particular, $f_{X|Y}(x|.3)=\frac{12x^2}{1.372}$ for $0<y<.7$. This is not one of the named distributions that we learned.

We can see that $X$ and $Y$ by either noting that $f_{Y|X}(y|x)\ne f_Y(y)$ or that $f_{X|Y}(x|y)\ne f_X(x)$.

23.4 Further Examples

Example 23.7 (Lifetimes of light bulbs) You buy two identical light bulbs of the same brand and type. The lifetimes of the light bulbs are independent and identically distributed (i.i.d.) random variables $X$ and $Y$.

Suppose we model their lifetimes (in years) by $\text{Exponential}(\lambda =0.4)$ distributions. Then, their joint PDF, by Definition 23.2, is $$f(x,y)=0.4e^{-0.4x}\cdot 0.4e^{-0.4y}$$ for $x,y>0$.

What is the probability that the first light bulb lasts shorter than the second, $P(X<Y)$? This event is sketched in Figure 23.8.

Figure 23.8: Probability that the first light bulb lasts shorter than the second.

We can calculate this probability by setting up a double integral: $$\begin{array}{rl}P(X<Y)& ={\int }_0^{\mathrm{\infty }}{\int }_x^{\mathrm{\infty }}0.4e^{-0.4x}\cdot 0.4e^{-0.4y}dydx\\ & ={\int }_0^{\mathrm{\infty }}0.4e^{-0.4x}\underset{e^{-0.4x}}{\underbrace{{\int }_x^{\mathrm{\infty }}0.4e^{-0.4y}dy}}dx\\ & ={\int }_0^{\mathrm{\infty }}0.4e^{-0.8x}dx\\ & =\frac{1}{2}.\end{array}$$

In hindsight, this answer was obvious by symmetry. Since the two light bulbs are identical, there is no reason that one light bulb should be more likely to last longer than the other. Therefore, $P(X<Y)=P(Y<X)$, and since $P(X=Y)=0$ for continuous random variables, these two events must each have probability $\frac{1}{2}$.

Example 23.7 illustrates that there is usually a way to avoid double integrals in most practical problems. When the distribution is uniform, as in Example 23.1, the probability can be calculated geometrically. When the random variables are i.i.d., we can appeal to symmetry. We will see more techniques in the upcoming chapters.

Example 23.8 (Three light bulbs) What if in Example 23.7, there had been three identical light bulbs, whose lifetimes $X$, $Y$, and $Z$ are i.i.d.? What is $P(X<Y<Z)$?

To calculate this by integration, we would need to set up a triple integral over their joint PDF, $f_{X,Y,Z}(x,y,z)$.

Instead, we will appeal to symmetry. $X<Y<Z$ is only one possible ordering of the lifetimes of the three light bulbs, but there are other possible orderings, such as $Y<Z<X$ or $Z<Y<X$. By symmetry, no ordering should be more likely than any other. So all of the orderings are equally likely and $$P(X<Y<Z)=\frac{1}{3!}=\frac{1}{6}.$$

The next example is a surprising application of joint PDFs. In Section 22.3, we saw that the PDF of the standard normal distribution is $$f_Z(x)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2},-\mathrm{\infty }<x<\mathrm{\infty }.$$ Where does the normalizing constant $1/\sqrt{2\pi }$ come from? To answer this question, we will first make the problem more complicated by considering the joint distribution of two independent standard normal random variables.

Example 23.9 (Normalizing constant of the standard normal) Determining the normalizing constant $k$ of the standard normal is not straightforward because there is no “simple” expression for the indefinite integral $\int e^{-x^2/2}dx$. (If you don’t believe it, try to find the antiderivative!)

The solution is to introduce two independent standard normal random variables. Let’s call them $X$ and $Y$. Because they are independent, their joint PDF must be the product of the marginal PDFs: $$f(x,y)=f_X(x)\cdot f_Y(y)=\frac{1}{k}{e}^{-x^2/2}\cdot \frac{1}{k}{e}^{-y^2/2}=\frac{1}{k^2}{e}^{-(x^2+y^2)/2}.$$ As we saw above, the total volume under any joint PDF must equal one.

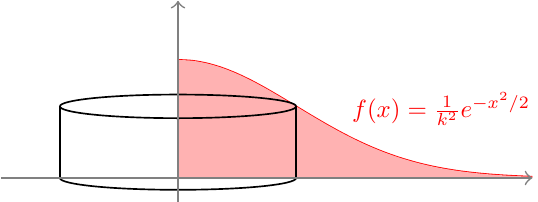
But this volume can be obtained as a solid of revolution! Specifically, the solid under this curve can be obtained by rotating the red shaded region in Figure 23.9 around the vertical axis.

Figure 23.9: The red region can be rotated around the vertical axis to obtain the solid under $\frac{1}{k^2}{e}^{-x^2+y^2}$.

The volume of this solid of revolution is most easily calculated using cylindrical shells. Each shell has a height of $f(x)=\frac{1}{k^2}{e}^{-x^2/2}$ and a base with area $2\pi xdx$, so the total volume is $$\begin{array}{rl}\text{Total Volume}& ={\int }_0^{\mathrm{\infty }}\frac{1}{k^2}{e}^{-x^2/2}\cdot 2\pi xdx\\ & =\frac{2\pi }{k^2}{\int }_0^{\mathrm{\infty }}{e}^{-x^2/2}\cdot xdx\\ & =\frac{2\pi }{k^2}{[-e^{-x^2/2}]}_0^{\mathrm{\infty }}\\ & =\frac{2\pi }{k^2}.\end{array}$$ Since we know the total volume must be one, we can solve for $k$: $$\begin{array}{rlrlrl}\frac{2\pi }{k^2}& =1& ⟹& & k& =\sqrt{2\pi }.\end{array}$$