The Art of Chance
A Beginner’s Guide to Probability
Preface
This textbook was designed for a two-quarter undergraduate sequence in probability (and some statistics) at Stanford University.
Why this Book?
There are already many introductory probability textbooks. Why another one?
We wrote this book to address two primary problems that we faced at Stanford, which we imagine that many other institutions face:
- The consensus probability curriculum, represented by books such as Ross (2020, chaps. 1–8) and Blitzstein and Hwang (2019, chaps. 1–10), is too ambitious for a 10-week quarter. (It was designed for a 15-week semester.)
- The consensus probability curriculum requires multivariable calculus and linear algebra, which excludes students in fields such as biology and economics from taking probability.
This book aims to be a stepping stone for these students; the first part of this book only assumes single-variable calculus and includes many applied and numerical examples, while still providing a rigorous foundation for mathematics, statistics, and data science majors and minors. The second part of this book provides technical depth for majors and minors.
At Stanford, we cover the contents of this book in two courses:
- The first course corresponds to the first half of this book, “Concepts and Applications”, which is a self-contained treatment of the essentials of probability. The intuition, the problem solving techniques, and the many applications are all here, as are the puzzles and paradoxes that make the subject lively.
- This part only assumes single-variable calculus, making it more accessible to students who may not have multivariable calculus and even to an advanced high-school student who has taken AP Calculus.
- The second course corresponds to the second half of this book, “Theory and Techniques”. We introduce some elements of statistical inference (maximum likelihood estimators, bias and variance, hypothesis testing), and use these to motivate abstract probability concepts, such as convolutions, limit theorems, and order statistics.
- This part of the book assumes multivariable calculus and linear algebra, both of which are necessary for a comprehensive understanding of probability and statistics. Linear algebra is not used until the “Multivariate Distributions” unit, so it is possible to take linear algebra concurrently with a course covering this material.
Distinguishing Features
In addition to the considerations above, we made several other pedagogical decisions in writing this book. We highlight some of these below.
- We first cover all of discrete probability, followed by all of continuous probability (although the book need not be read this way, see below). This means that every concept is treated twice, once for discrete random variables and again for continuous random variables.
- We find that difficult concepts, such as joint distributions and conditional expectation, are easier to grasp if they are first introduced in the context of discrete probability, without the added complication of calculus.
- One concern is that by separating discrete and continuous random variables, learners may fail to see the connections between them. To help make these connections, the structure of the continuous chapters mirror the structure of the discrete chapters, with explicit signposting in the continuous chapters directing the reader to the corresponding results for discrete random variables. Also, the final chapters, 26 From Conditionals to Marginals and 27 Conditional Expectations, feature examples that mix discrete and continuous random variables, preparing learners to apply concepts in both settings.
- Calculus is de-emphasized in favor of arguments that offer more statistical intuition. For example:
- The famous continuous families (uniform, exponential, normal) can all be derived from location-scale transformations of a single representative. So we only need to derive the expectation and variance of a representative member of the family, and the general formula can be obtained using properties of expectation.
- Although we introduce double integrals for the sake of completeness, we show how geometry, symmetry, and conditioning allow us to avoid multiple integrals (or calculus altogether!). See 23 Joint Distributions and 24 Expectations Involving Multiple Random Variables for examples.
- We favor models that are specified hierarchically (i.e., by specifying first the distribution of \(X\), then the conditional distribution of \(Y | X\)), rather than jointly. We dedicate two entire chapters, 16 From Conditionals to Marginals and 26 From Conditionals to Marginals, to the use of Law of Total Probability for such models, which are omitted in many textbooks or treated as an afterthought.
- Hierarchical specifications are more common in statistics, especially in Bayesian statistics.
- Hierarchical models provide a more natural way to describe “mixed” distributions that are neither discrete nor continuous.
- The derivations of the gamma-beta connection (Proposition 41.3) and the \(t\)-distribution (Proposition 46.1) are illustrations of this approach. In our opinion, these derivations are more “statistical” than the standard derivation using Jacobians.
- Code snippets in the programming language R are integrated into the exposition of the book.
- R is used to do simulations to motivate concepts.
- R is used to perform calculations that are impractical to do by hand. In the online version of this book, the R snippets can even be run in the browser.
- In addition to applications from different disciplines, we have included many historical examples, such as the problem of points (Example 1.10), Pascal’s wager (Example 9.5), and the German Tank Problem (31.1 German Tank Problem).
How to Use this Book?
For Instructors
Part I
Each chapter can be covered thoroughly in an 80-minute lecture or outlined in a 50-minute lecture. At Stanford, we cover this material in a 10-week quarter with three 50-minute lectures per week. Schools on a 15-week semester system would be able to cover this material more completely (or include a selection of topics from Part II).
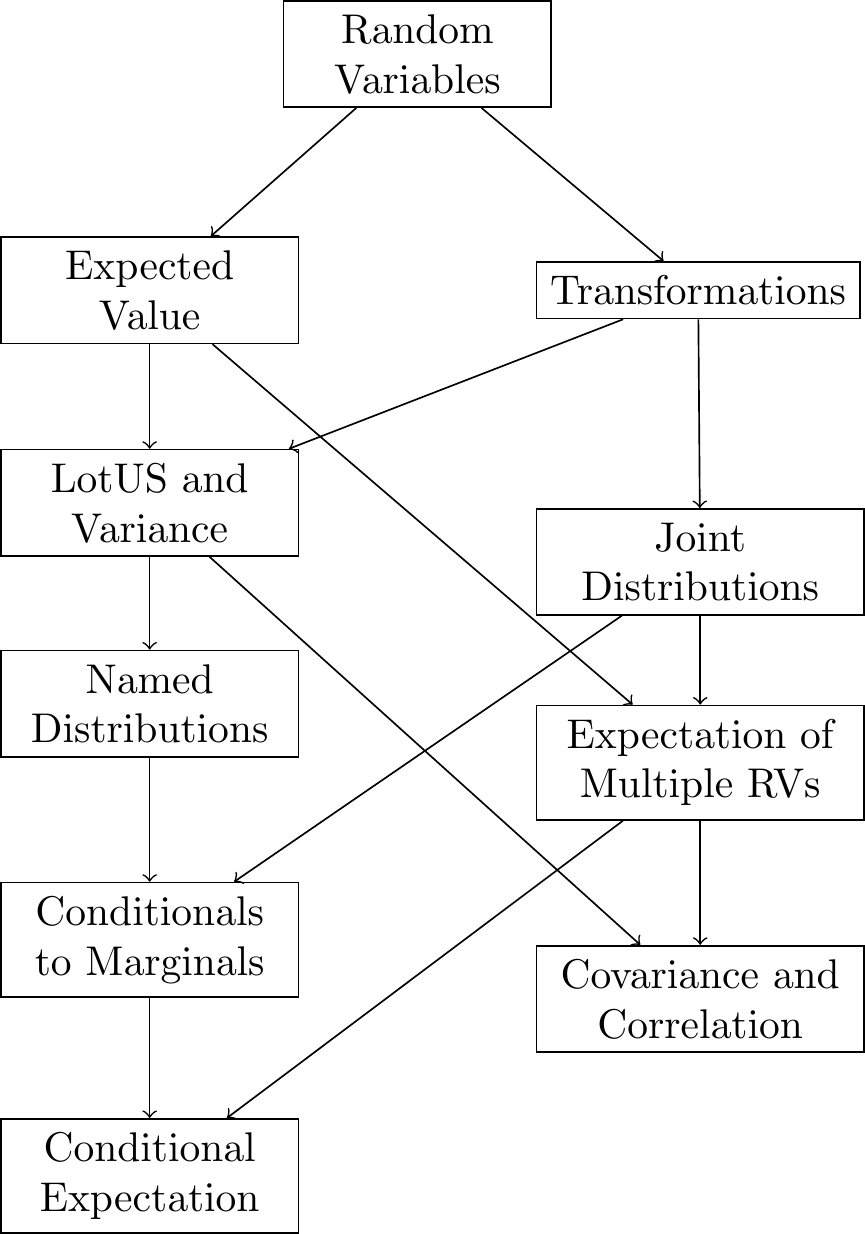
We have designed the book to be modular so that chapters can be read in any (reasonable) order. For example, one pedagogical question is whether joint distributions should be covered before or after expected value. We have written those chapters so that they can be read in either order. The dependency graph illustrates the relationships between the chapters in the discrete and continuous sections, in case you wish to cover the chapters in an order different from ours.
Compared to other probability textbooks that we have used in the past, Part I covers the equivalent of:
- Ross (2020), Chapters 1, 2, 3, 4, 5.1-5.5, 6.1-6.5, 7.1-7.6, 8.1-8.2
- Blitzstein and Hwang (2019), Chapters 1, 2, 3, 4, 5, 7.1-7.3, 9, 10.1-10.2
Common topics in introductory probability that are not covered in Part I, but are instead deferred to Part II, include:
- gamma and beta distributions (because the gamma function is difficult for many students)
- multivariate normal distribution (because it requires linear algebra)
- Jacobian transformations (because they require multivariable calculus)
- moment generating functions (because they are too abstract for most students)
- Central Limit Theorem (because we cannot prove it without MGFs)
Part II
Each chapter is designed to be covered in one 80-minute lecture. At Stanford, we cover this material in a 10-week quarter with two 80-minute lectures per week.
A 15-week semester probability course, with approximately forty 50-minute lectures, might be able to cover all of Part I, in addition to Chapters 29-38. This covers all the topics in a “traditional” probability course, except for order statistics (39 Minima and Maxima, 40 General Order Statistics), the beta distribution (41 Beta Distribution) and Jacobians (42 Multivariate Transformations). The chapters on “Estimation Theory” are unconventional for a pure probability course, but they really provide excellent motivation for concepts that many students find abstruse, such as limit theorems.
Part Three?
As far as we are aware, there are only a few topics covered in a typical undergraduate mathematical statistics sequence that are not covered here:
- Fisher information and the Cramer-Rao inequality
- Sufficiency and the Rao-Blackwell theorem
- Neyman-Pearson lemma and likelihood ratio tests
- Resampling methods for inference (e.g., bootstrap, permutation test)
At Stanford, these topics are covered in the third quarter. However, it may be argued (and many of our students have reported to us) that a student with a solid understanding of this book will find those topics to be minor extensions. In our opinion, this book provides a necessary and sufficient background in theoretical statistics for an undergraduate major in Data Science and Statistics.
For Students
This book is meant to be read. We have tried to choose examples that we think you will find interesting.
Definitions, theorems, and examples all appear in colored boxes. Proofs are included inside the box for the corresponding theorem. When a proof is not important, it is collapsed. We recommend that you skip proofs that are collapsed, especially on a first reading, unless you are interested.
You should run the code that is provided and try modifying it to see what it does.
Acknowledgements
Our colleagues provided feedback which improved this book, including John Duchi, Trevor Hastie, Jessica Hwang, Shuangping Li, Chiara Sabatti, Tony Samuel, Timothy Sun, and Guenther Walther.
Several students in our courses also provided useful feedback, including Nacho Fernandez, Jack Hlavka, Mark Leschinsky, Chenyue Qian, Ricky Rojas, Duru Unsal, and Viet Vu.
The influence of teachers and colleagues who have shaped the way we teach probability is unmistakable. Thank you to Joe Blitzstein, Matt Carlton, Kevin Ross, and Allan Rossman.
We also acknowledge the support of a Curriculum Transformation Seed Grant from the Stanford Vice Provost for Undergraduate Education and Center for Teaching and Learning, which funded the writing of this book.