30  The Calculus of Maximum Likelihood

In Chapter 29, we saw how the MLE enables us to learn about unknown parameter(s) of the underlying distribution from the observed data. As we saw, however, finding the MLE can involve somewhat lengthy computations.

In this chapter, we present a standard strategy for finding MLEs that often greatly simplifies the required computation. By the end of the chapter, you will be well equipped to compute MLEs in a wide variety of problems!

30.1 The Log-Likelihood

At the end of Chapter 29, we computed the MLE for \(p\) after observing a random variable \(X\) with \(\text{Binomial}(n, p)\) distribution. Because \(p \in [0,1]\) has continuous range of possible values and the likelihood

\[ L_{x}(p) = \binom{n}{x} p^x (1 - p)^{n - x}. \]

is a differentiable function of \(p\), we did this by taking the derivative of the likelihood with respect to \(p\) and setting it equal to zero. This computation, however, was a bit nastier than it needed to be. Most likelihoods we encounter will be a product of terms involving the unknown parameter(s). Taking the derivative of the likelihood with respect to the unknown parameter(s) therefore requires the product rule, which can be cumbersome and messy. If we instead take the log of the likelihood, we get

\[\begin{align*} \ell_x(p) &= \log(L_{x}(p))\\ &= \log\left(\binom{n}{x} p^x (1 - p)^{n - x}\right) \\ &= \log \binom{n}{x} + x \log p + (n-x) \log(1-p), \end{align*}\] which is a sum instead of a product. The log of the likelihood is aptly named the log-likelihood.

Definition 30.1 (Log-likelihood) Suppose we observe data \(X\) that has PMF (or PDF) \(f_\theta(x)\) for some unknown parameter(s) \(\theta\). The log-likelihood of \(\theta\) is defined as \[ \ell_{x}(\theta) = \log(L_{x}(\theta)) = \log(f_\theta(x)), \tag{30.1}\]

where \(L_x(\theta)\) is the likelihood of \(\theta\) (Definition 29.1).

Since \(\log(\cdot)\) is a monotonic function (larger values of \(y\) result in a larger values of \(\log(y)\)), the value of \(\theta\) that maximizes the log-likelihood also maximizes the likelihood. Since the derivative of a sum is the sum of the derivatives, finding the \(\theta\) that maximizes the log-likelihood is usually computationally easier.

Example 30.1 redoes our MLE computation for the binomial likelihood, but this time maximizes the log-likelihood. Although the computation is similarly lengthy, it is cleaner, and each individual step is much simpler.

Example 30.1 (Binomial MLE via the log-likelihood) Suppose we observe data \(X\) which has a \(\text{Binomial}(n, p)\) distribution. What is the MLE for \(p\)?

We consider the log-likelihood

\[ \ell_x(p) = \log \binom{n}{x} + x \log p + (n-x) \log(1-p). \]

To find the \(p\) that maximizes \(\ell_x(\theta)\), we differentiate \(\ell_x(\theta)\) with respect to \(p\):

\[\begin{align*} \frac{\partial}{\partial p} \ell_{x}(p) &= \frac{\partial}{\partial p} \log \binom{n}{x} + x \cdot \frac{\partial}{\partial p} \log p + (n-x) \cdot \frac{\partial}{\partial p} \log(1-p) \\ &= \frac{x}{p} - \frac{n-x}{1-p}. \end{align*}\]

The MLE \(\hat{p}\), which is the value of \(p\) that maximizes \(\ell_x(p)\), sets this derivative to zero. Solving \[ \frac{x}{\hat{p}} - \frac{n-x}{1-\hat{p}} = 0 \] leads to \[ x - n \hat{p} = 0 \] from which we conclude that \[ \hat{p} = \frac{x}{n}. \]

Example 30.2 provides another example of how working with log-likelihoods makes it easier to find MLEs.

Example 30.2 (Geometric MLE via the log-likelihood) Your friend claims to be an excellent free throw shooter. You’re a bit skeptical, so they tell you that the last time they practiced their free throws, they made seven in a row before missing their eighth. Assuming the free throws are independent and your friend had the same probability of making each one, what is a good estimate for their probability \(p\) of making a free throw?

Because your friend shot free throws until missing, the (random) number of free throws \(X\) they took has a \(\text{Geometric}(1 - p)\) distribution (Definition 8.7). To get an estimate, we find the MLE of \(p\) for the observed data \(X = \textcolor{blue}{8}\). The likelihood function is given by

\[ L_{\textcolor{blue}{8}}(p) = p^{\textcolor{blue}{8} - 1}(1-p). \]

Correspondingly, the log-likelihood function is \[ \ell_8(p) = (\textcolor{blue}{8} -1) \log p + \log(1-p) \] whose derivative is

\[ \frac{\partial}{\partial p} \ell_{8}(p) = \frac{(\textcolor{blue}{8} -1)}{p} - \frac{1}{1-p} \]

The MLE \(\hat{p}\), which maximizes \(\ell_X(\theta)\), sets this derivative to zero; solving the appropriate equations leads to

\[ \hat{p} = \frac{\textcolor{blue}{8} -1}{\textcolor{blue}{8}} = \frac{7}{8}. \]

In general, if your friend’s first miss happens on free throw \(X\), the MLE estimate of \(p\) would be

\[\hat{p} = \frac{X - 1}{X} = 1 - \frac{1}{X}. \]

The MLE for \(p\) in Example 30.2 is the number of made free throws over the number of total free throws, very similar to the binomial case. In fact, if our friend told us that they made seven out of eight free throws instead of telling us that they made seven free throws before missing one, the MLE for \(p\) would remain the same. The data generating distribution in these two cases, however, is not the same (one is binomial while the other is geometric).

Example 30.3 gives another example where it is easier to work with the log-likelihood in place of the likelihood. It also clearly illustrates an important point: when working with continuous random variables, likelihoods and probabilities are not the same.

Example 30.3 (Normal MLE via the log-likelihood) Suppose \(X \sim \text{Normal}(\mu, \textcolor{red}{0.3^2})\). If we observe \(X = \textcolor{blue}{3}\), what is the MLE for \(\mu\)?

The below code plots the likelihood function, which is given by \[ L_{\textcolor{blue}{3}}(\mu) = \frac{1}{\textcolor{red}{0.3} \cdot \sqrt{ 2 \pi}} e^{-(\textcolor{blue}{3} - \mu)^2/(2 \cdot \textcolor{red}{0.3}^2 ) }. \]

The likelihood of \(\mu\) appears to be maximized at our observed value \(X = \textcolor{blue}{3}\). Given that the normal PDF achieves its peak at the mean, this should not be too surprising.

Let us now explicitly show that the MLE is \(\hat{\mu}= \textcolor{blue}{3}\). The log-likelihood

\[ \ell_{\textcolor{blue}{3}}(\mu) = -\frac{1}{2}\log(\textcolor{red}{0.3}^2) -\frac{1}{2}\log(2\pi) - \frac{(\textcolor{blue}{3} - \mu)^2}{2\cdot \textcolor{red}{0.3}^2 } \]

is much easier to study. It is clear that the log-likelihood achieves its maximum value when \(-\frac{1}{2}\log(\textcolor{red}{0.3}^2) -\frac{1}{2}\log(2\pi)\) when we plug in \(\mu = \textcolor{blue}{3}\). If we plug in any other value, the term \((\textcolor{blue}{3} - \mu)^2\) will be positive and the overall log-likelihood will be smaller. Hence, the MLE is \(\hat{\mu}= 3\).

In general, our argument implies that, regardless of what value of \(X\) we observe, the MLE is given by \(\hat{\mu} = X\).

Likelihoods are not probabilities

When we are working with continuous random variables, likelihoods are not probabilities. We can see from the plot that, in this problem, the likelihood of \(\mu=3\)

\[ \ell_{\text{3}}(3) \approx 1.26 \]

is greater than one! It is best to think of likelihoods and probabilities as two conceptually distinct ideas. The former is used to infer something about the unknown data generating distribution, while the latter is the chance of something happening under some (often known) data generating distribution.

30.2 Estimation from a Random Sample

In practice, we rarely observe a single data point \(X\), but an entire data set \(X_1, \dots, X_n\). One basic model for a data set is a random sample. In a random sample, the random variables \(X_1, \dots, X_n\) are assumed to be independent and identically distributed, or i.i.d. for short.

When random variables \(X_1, \dots, X_n\) are i.i.d., they all have the same PMF (or PDF) \(f_{\theta}(x)\) and, due to independence, their joint PMF (of PDF) factors (recall Definition 13.2 and Definition 23.2):

\[ f_{\theta}(x_1, \dots, x_n) = f_{\theta}(x_1) f_{\theta}(x_2) \cdots f_{\theta}(x_n). \]

The likelihood of \(\theta\) for the observed data \(x_1, \dots, x_n\) is hence always a big product, \[ L_{x_1, \dots, x_n}(\theta) = f_{\theta}(x_1) f_{\theta}(x_2) \cdots f_{\theta}(x_n), \] which is why the log-likelihood comes in handy. Taking logarithms turns the product into a sum: \[ \ell_{x_1, \dots, x_n}(\theta) = \log(f_{\theta}(x_1)) + \cdots + \log(f_{\theta}(x_n)), \] Because the subscript starts to become cumbersome with \(n\) data points, we will often omit it and simply write the likelihood and log-likelihood as \(L(\theta)\) and \(\ell(\theta)\) respectively.

Our first example generalizes Example 30.3 by supposing we observe many i.i.d normal samples with unknown variance.

Example 30.4 (Normal MLE via the log-likelihood) Suppose \(X_1, \dots, X_n\) are i.i.d. \(\text{Normal}(\mu, \sigma^2)\), where \(\mu\) and \(\sigma^2\) are unknown. What are the MLEs for \(\mu\) and \(\sigma^2\)?

Due to independence, the likelihood for a \(\mu\) and \(\sigma^2\) pair is given by the product

\[ L(\mu, \sigma^2) = f_{\mu, \sigma^2}(x_1, \dots, x_n) = \prod_{i=1}^n f_{\mu, \sigma^2}(x_i), \] where \(f_{\mu, \sigma^2}\) is the PDF of a normal random variable with mean \(\mu\) and variance \(\sigma^2\).

Per usual, rather than deal with the product, we instead examine the log-likelihood. Using our above computations and our earlier work from Example 30.3, we find that the log-likelihood is

\[ \ell(\mu, \sigma^2) = -\frac{n}{2}\log(2\pi) -\frac{n}{2}\log \sigma^2 - \frac{1}{2 \sigma^2 } \sum_{i=1}^n (x_i - \mu)^2. \]

Our computations from Example 30.3 imply that

\[ \log f_{\mu, \sigma^2}(x_i) = \left(-\frac{1}{2}\log(2\pi) -\frac{1}{2}\log(\sigma^2) - \frac{1}{2 \sigma^2 }(x_i - \mu)^2 \right) \]

Using this fact, we can write down the log-likelihood.

\[\begin{align*} \ell(\mu, \sigma^2) &= \log L(\mu, \sigma^2) & \text{(definition of log-likelihood)}\\ &= \log \left( \prod_{i=1}^n f_{\mu, \sigma^2}(x_i)\right) & \text{(definition of likelihood)}\\ &= \sum_{i=1}^n \log f_{\mu, \sigma^2}(x_i) & \text{(properties of log)}\\ &= \sum_{i=1}^n \left( -\frac{1}{2}\log(2\pi) -\frac{1}{2}\log \sigma^2 - \frac{1}{2 \sigma^2 }(x_i - \mu)^2 \right) & \text{(earlier computation)}\\ &= -\frac{n}{2}\log(2\pi) -\frac{n}{2}\log \sigma^2 - \frac{1}{2 \sigma^2 } \sum_{i=1}^n (x_i - \mu)^2 & \text{(simplify)} \end{align*}\]

The MLEs for \(\mu\) and \(\sigma^2\) are the pair \(\hat{\mu}\) and \(\hat{\sigma}^2\) that jointly maximize this log-likelihood. Hence, they must set both the partial derivatives to zero:

\[\begin{align*} \frac{\partial}{\partial \mu} \ell(\hat{\mu}, \hat{\sigma}^2) &= 0 \\ \frac{\partial}{\partial \sigma^2} \ell(\hat{\mu}, \hat{\sigma}^2) &= 0 \end{align*}\]

We compute these partial derivatives one at a time.

MLE of \(\mu\): We start with the partial derivative with respect to \(\mu\):

\[ \frac{\partial}{\partial \mu} \ell(\mu, \sigma^2) = \frac{1}{\sigma^2} \left( \left( \sum_{i=1}^n X_i \right) - n\mu \right) \]

\[\begin{align*} \frac{\partial}{\partial \mu} \ell(\mu, \sigma^2) &= \frac{\partial}{\partial \mu} \left( -\frac{n}{2}\log(2\pi) -\frac{n}{2}\log \sigma^2 - \frac{1}{2 \sigma^2 } \sum_{i=1}^n (x_i - \mu)^2 \right) \\ &= - \frac{\partial}{\partial \mu}\frac{n}{2}\log(2\pi) - \frac{\partial}{\partial \mu} \frac{n}{2}\log \sigma^2 - \frac{\partial}{\partial \mu}\frac{1}{2 \sigma^2 } \sum_{i=1}^n (x_i - \mu)^2 \\ &= \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) \\ &= \frac{1}{\sigma^2} \left( \left( \sum_{i=1}^n X_i \right) - n\mu \right).\\ \end{align*}\]

Setting the above partial derivative equal to \(0\) yields \[ \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i. \]

We have determined the MLE for \(\mu\), but we know nothing about the MLE for \(\sigma^2\).

MLE of \(\sigma^2\): To find the MLE for \(\sigma^2\), we take the partial derivative with respect to \(\sigma^2\):

\[ \frac{\partial}{\partial \sigma^2} \ell(\mu, \sigma^2) = \frac{1}{2\sigma^4} \left( \sum_{i=1}^n (x_i - \mu)^2 - n\sigma^2 \right) \]

\[\begin{align*} \frac{\partial}{\partial \sigma^2} \ell(\mu, \sigma^2) &= -\frac{\partial}{\partial \sigma^2}\frac{n}{2}\log(2\pi) - \frac{\partial}{\partial \sigma^2} \frac{n}{2}\log \sigma^2 - \frac{\partial}{\partial \sigma^2} \frac{1}{2 \sigma^2} \sum_{i=1}^n (x_i - \mu)^2 \\ &= - \frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 \\ &= \frac{1}{2\sigma^4} \left( \sum_{i=1}^n (x_i - \mu)^2 - n\sigma^2 \right) \\ \end{align*}\]

The MLEs \(\hat{\mu}\) and \(\hat{\sigma}^2\) must also set this derivative to zero, and thus satisfy

\[\begin{align*} & \frac{1}{2\hat{\sigma}^4} \left( \sum_{i=1}^n (X_i - \hat{\mu})^2 - n\hat{\sigma}^2 \right) = 0 & \text{(set derivative to zero)} \\ & \iff \sum_{i=1}^n (X_i - \hat{\mu})^2 - n\hat{\sigma}^2 = 0 & \text{(multiply both sides by $2\hat{\sigma}^4$)} \\ & \iff \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \hat{\mu})^2 & \text{(solve for \(\hat{\sigma}^2\))}. \end{align*}\]

In the end we find that the MLEs are

\[\begin{align*} \hat{\mu} &= \frac{1}{n}\sum_{i=1}^n X_i \\ \hat{\sigma^2} &= \frac{1}{n} \sum_{i=1}^n (X_i - \hat{\mu})^2 \end{align*}\]

Our next example involves finding the MLE when we observe i.i.d. exponential random variables.

Example 30.5 (Exponential scale MLE via the log-likelihood) Suppose we observe \(X_1, \dots, X_n\) that are \(\text{Exponential}(\lambda)\) (Definition 22.2). What is the MLE for \(\lambda\)?

This time, we will simply start by computing the log-likelihood

\[\begin{align*} \ell(\lambda) &= \sum_{i=1}^n \log(\lambda e^{-\lambda x_i}) & \text{(exponential density)}\\ &= \sum_{i=1}^n \left( \log(\lambda) -\lambda x_i \right) & \text{ (log properties) }\\ &= n \log(\lambda) - \lambda \sum_{i=1}^n x_i. \end{align*}\]

The MLE \(\hat{\lambda}\) sets the derivative of the log-likelihood to zero. The derivative of the log-likelihood is

\[ \frac{\partial\ell}{\partial \lambda} = \frac{n}{\lambda} - \sum_{i=1}^{n} x_i. \]

Setting this derivative equal to zero and solving for \(\lambda\) yields

\[ \hat{\lambda} = \frac{n}{\sum_{i=1}^{n} x_i}. \]

The last example is a reminder of the importance of thinking before calculating. With some careful thinking, we can avoid most calculations.

Example 30.6 (Exponential location MLE) Let \(X_1, \dots, X_n\) be i.i.d. exponential with rate \(1\) and location parameter \(\theta\). That is, \(X_i\) can be represented as \[ X_i = \theta + Z_i, \] where \(Z_1, \dots, Z_n\) are i.i.d. \(\textrm{Exponential}(\lambda=1)\). (Note that we only observe \(X_i\), not \(Z_i\).)

The PDF of each \(X_i\) is given by: \[ f_{\mu}(x) = \begin{cases} e^{-(x - \theta)}, & x \geq \theta, \\ 0, & x < \theta. \end{cases} \tag{30.2}\] What is the MLE of \(\theta\)?

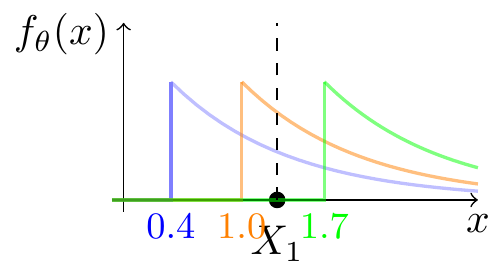
To gain some intuition, imagine that we observe \(X_1 = 1.3\), and consider the PDF Equation 30.2 for \(\theta = 0.4\), \(\theta = 1.0\), and \(\theta = 1.7\).

Figure 30.1: PDF for three values of \(\theta\)

Visually, we see that the likelihood of \(\theta = 1.0\) is greater than that of \(\theta = 0.4\). This is because the PDF is a decaying exponential, and the exponential has less “space” to decay when \(\theta\) is larger. On the other hand, if \(\theta\) is too large, the likelihood is actually zero, as we see when \(\theta = 1.7\). The sweet spot that maximizes the likelihood is to set \(\theta = X_1\), where the likelihood is nonzero and the exponential has not started to decay.

Now, returning to the setup of the original problem where we have a random sample \(X_1, \dots, X_n\) from this distribution. We want to make \(\theta\) as large as possible but no larger. If we choose a value of \(\theta\) that is greater than some \(X_i\), then the likelihood will be zero. In other words, we want to make \(\theta\) as large as possible, but we also want to ensure that \(\theta \leq \min(X_1, \dots, X_n)\). Therefore, the MLE is \[ \hat\theta = \min(X_1, \dots, X_n). \]

Notice that log-likelihoods and calculus are not helpful in this example. The key to the solution was analyzing where the likelihood is zero, and \(\log(0)\) is not defined. Furthermore, the likelihood is not differentiable at the point that matters most, when \(\theta = \min(X_1, \dots, X_n)\).

However, there is a way to solve for the MLE using mathematical notation. We can write the PDF Equation 30.2 using indicator functions \[ f_\theta(x) = e^{-(x - \theta)} 1\{ x \geq \theta \} \] so that the likelihood for the entire sample is \[ \begin{align} L_{x_1, \dots, x_n}(\theta) &= \prod_{i=1}^n e^{-(x_i - \theta)} 1\{ x_i \geq \theta \} \\ &= e^{- \sum_{i=1}^n x_i + n\theta} \prod_{i=1}^n 1\{ x_i \geq \theta \} \\ &= e^{- \sum_{i=1}^n x_i + n\theta} 1\{ \min(x_1, \dots, x_n) \geq \theta \}. \end{align} \]

From the first term, it is clear that likelihood can be maximized by making \(\theta\) as large as possible. However, the second term indicates that \(\theta\) cannot be any greater than \(\min(x_1, \dots, x_n)\), or else the likelihood will be zero.

30.3 Exercises

Exercise 30.1 Consider an i.i.d. sample (of size \(n\)) of random variables with density function \[ f(x) = \frac{1}{2\sigma} \exp\left( -\frac{\lvert x \rvert}{\sigma} \right) \] for \(-\infty < x < \infty\), where \(\sigma\) is unknown. Find the MLE of \(\sigma\).

Exercise 30.2 Let \(X_1, \dots, X_n\) be i.i.d. from a Rayleigh distribution with unknown parameter \(\theta > 0\): \[ f_\theta(x) = \frac{x}{\theta^2} e^{-\frac{x^2}{2\theta^2}} \] for \(x \geq 0\). Find the MLE of \(\theta\).

Exercise 30.3 Let \(X_1, \dots, X_n\) be i.i.d. with density \[ f(x) = (\theta + 1)x^\theta \] for \(0 \leq x \leq 1\), where \(\theta\) is unknown. Find the MLE of \(\theta\).

Exercise 30.4 Let \(X_1, \dots, X_n\) be i.i.d. \(\text{Uniform}(0,\theta)\), where \(\theta\) is unknown. Find the MLE of \(\theta\).

Exercise 30.5 The double exponential distribution has density \[ f(x) = \frac{1}{2} e^{-\lvert x - \theta \rvert} \] for \(-\infty < x < \infty\). For an i.i.d. sample of size \(n = 2m + 1\) (\(n\) is odd), show that the MLE of \(\theta\) is the median of the sample.

Remark. The function \(\lvert x \rvert\) is not differentiable. Once you find an appropriate quantity to minimize, it may help to draw pictures for small values of \(n\) (such as \(3\)) to understand the behavior of the said quantity.